2.4 Третий признак равенств треугольников

Если три стороны первого треугольника равны трём сторонам второго треугольника соответственно, то эти два треугольника равны между собой.

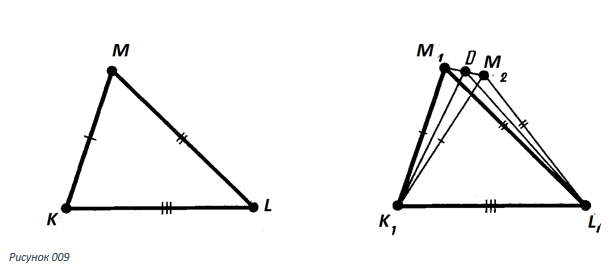
Доказательство. Пусть KLM и K₁L₁M₁ это два данных треугольника. K₁L₁=KL, K₁M₁=KM, L₁M₁=LM на рисунке 009. Надо доказать, что первый треугольник равен второму.

Предположим, что они НЕ равны. Тогда у них соответствующие углы не будут равны. Тогда эти треугольники были бы равны по первому признаку.

Пусть K₁L₁M₂ – треугольник, который равен треугольнику KLM, у которого M₂ лежит в одной полуплоскости с вершиной M₁ относительно прямой K₁L₁.

Тогда D будет серединой отрезка M₁M₂. Треугольники K₁M₁M₂ и L₁M₁M₂ будут равнобедренными с основанием M₁M₂. Прямые K1D и L1В не будут совпадать, так как точки K1, L1, В не лежат в одной прямой. А через точку D принадлежащей M1M2, можно провести только одну перпендикулярную прямую. Мы столкнулись с противоречием, значит теорема доказана.