4 Сумма углов треугольников

Теорема.

Сумма всех углов треугольника всегда равно ста восьмидесяти градусам.

Доказательство.

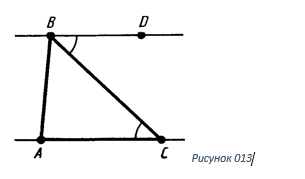
На рисунке 013 дан треугольник ABC. Проведя через вершину B прямую, которая будет параллельна прямой AC, отметим на ней точку D. Всё должно быть так, чтобы D и A лежали по разные стороны от прямой CB.

Угол ACB и угол DBC равны между собой как накрест лежащие, которые образовались секущей CB с параллельными прямыми BD и AC. Следовательно сумма всех углов треугольника при вершинах C и B равна углу DBA, а сумма всех углов треугольника равна сумме CAB и DBA. Следуя из того, что эти углы являются внутренними односторонними для параллельных прямых DB и CA и секущей BA, то их сумма равняется ста восьмидесяти градусам. Теорема доказана.

Из этой теоремы следует, что у всякого треугольника как минимум два угла острых. Действительно, предположим, что у треугольника только один угол острый или вовсе их нет, тогда у данного треугольника, есть два угла, каждый из которых не меньше девяносто градусов. Сумма этих двух углов станет уже не меньше 180 градусов. А такое не возможно, потому что сумма всех углов треугольника равна 180 градусам. Ч.т.д.