1.2 Определения треугольника «своими словами». Связь треугольника с другими многоугольниками (n-угольниками) в планиметрии

Ознакомившись с понятием треугольника, разобравшись с его обозначениями, его свойствами учащиеся смогут уже самостоятельно предлагать свои понятия о треугольнике. Ниже перечислены следующие определения, к которым пришли учащиеся школы, в которой я проходил производственную практику:

Треугольник – фигура, имеющая площадь бо?льшую нуля.

Треугольник – часть плоскости, ограниченная наименьшим числом сторон.

Треугольник – фигура, из которой можно составить любой n-угольник.

Данные выводы не являются и не могут быть определением треугольников, так как это всего лишь гипотезы и в них не достаточно информации. Но они выполняют одну из задач дипломной работы – приводят к такому выводу, что любой многоугольник и даже треугольник можно разбить на множество треугольников.

Треугольник, как и любой другой многоугольник можно построить как минимум в двумерном пространстве. А это означает, что у данной фигуры есть площадь – размер занимаемый часть плоскости.

Вычисляя точную площадь произвольного четырёхугольного участка, например, с разными сторонами, а значит и разными углами, можно столкнуться с такой сложностью, что в геометрии нет формулы для вычисления площади произвольных многоугольников (далее n-угольник).

В связи с этим необходимо выявлять какие-то свойства произвольных n-угольников.

Самое просто свойство – о нём уже говорилось выше – это то, что любой n-угольник можно разбить на бесконечное число треугольников. Это утверждение имеет место в решение подобных задач. Так как действительно, любой четырёхугольник возможно разбить, как минимум, на два треугольника, как максимум на множество треугольников.

Данный способ не гарантирует решение задач на 100 процентов. Так как чтобы вычислить площадь треугольника необходимо знать хотя бы три его параметра (в решении треугольников значение только трёх углов будет недостаточно, так как с такими же параметрами может существовать бесконечное число других треугольников, подобных данному).

Зная все свойства треугольников можно вычислить площадь произвольного четырёхугольника по частям, если будет достаточное условие. Во внимание следует брать такие свойства, как признаки равенства, подобия, несуществования треугольников, теоремы синусов, косинусов (в частности Теорема Пифагора), необходимо знать правила нахождения площади треугольников, так же полезны могут быть знания свойств высот, медиан, биссектрис треугольника.

Для этого нужно повторить все пройденные темы.

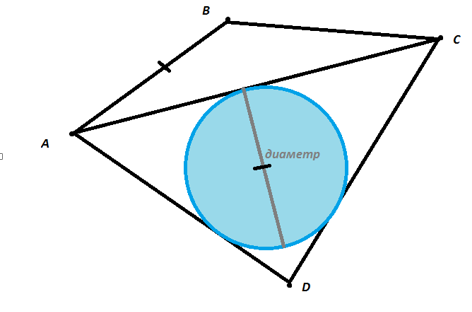
Рисунок 003