7 Окружности, вписанные в треугольники

Окружности, называются вписанными в треугольники, если они касаются всех сторон треугольника.

Теорема.

Центры окружностей, вписанных в треугольники, являются точками пересечения их биссектрис.

Доказательство.

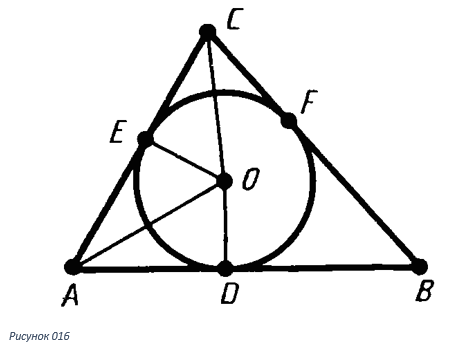
На рисунке 016 дан треугольник CBA, в который вписана окружность с центром в точке 0. F, E и D это точки касания сторон треугольника и окружности. Прямоугольные треугольники DOA и EOA равны по катету и гипотенузе. Там гипотенуза 0A общая, и катеты E0 и D0 равны как радиусы. Следовательно из равенств треугольников выполняется равенство угла DAO и угла EAO. Значит точка 0 лежит на биссектрисе, которую провели из точки А. Таким же способом доказывается, что точка 0 лежит на других биссектрисах. Ч.т.д.